Machine Learning Compiler Deep Neural Network Tensor Computation

TensorIR ASPLOS 2023

TensorIR An Abstraction for Automatic Tensorized Program Optimization

Posted by Treaseven on December 10, 2024

Motivation

  • 现代硬件加速器引入专门的张量计算原语
  • 传统手动优化库开发成本高，难以适应快速变化的模型和硬件
  • 需要自动化编译方法来利用这些硬件加速能力 面临的挑战 (1) Abstraction for Tensorized Programs：需要一个能表达等价张量化计算的抽象 (2) Large Design Space of Possible Tensorized Program Optimizations：需要在大规模设计空间中找到优化方案 提出TensorIR (1) 引入block构造来分离张量计算 (2) 构建具有正确性验证的变换原语 (3) 设计新的张量化感知自动调度器

Overview

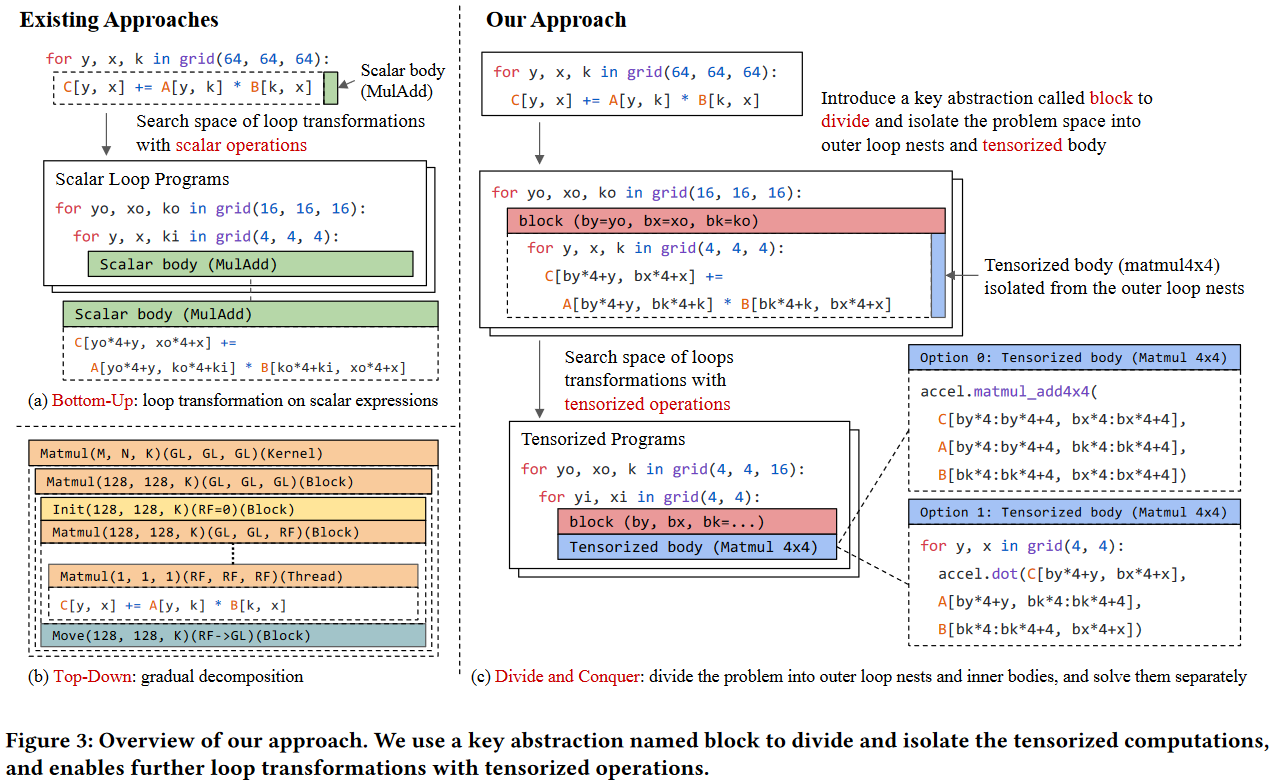
TensorIR Abstraction

Block

Scheduling Transformations

可调度性的定义
(1) 一个block是”可调度的”.如果它只包含以子block作为叶节点的循环嵌套
(2) 通过分析子block的签名核依赖信息来转换这些可调度block中的循环嵌套
(3) 可调度block可以包含不可调度的子block

schedule primitive

  • Loop Transformations
  • Blockization
  • Separation of Scheduling and TensorIR

Validation

Loop Nesta Validation: 验证迭代器绑定是否满足迭代域约束
Threading Validation: 线程绑定、协作内存访问、执行作用域
Correctness of Schedule Primitives: 当原语只改变循环嵌套时可以用于验证过程确保正确性；对于blocks的原语找到原语特定的必要条件

Auto-Scheduling Tensorized Programs

  • 识别张量计算机会
  • 构建程序框架
  • 优化具体参数 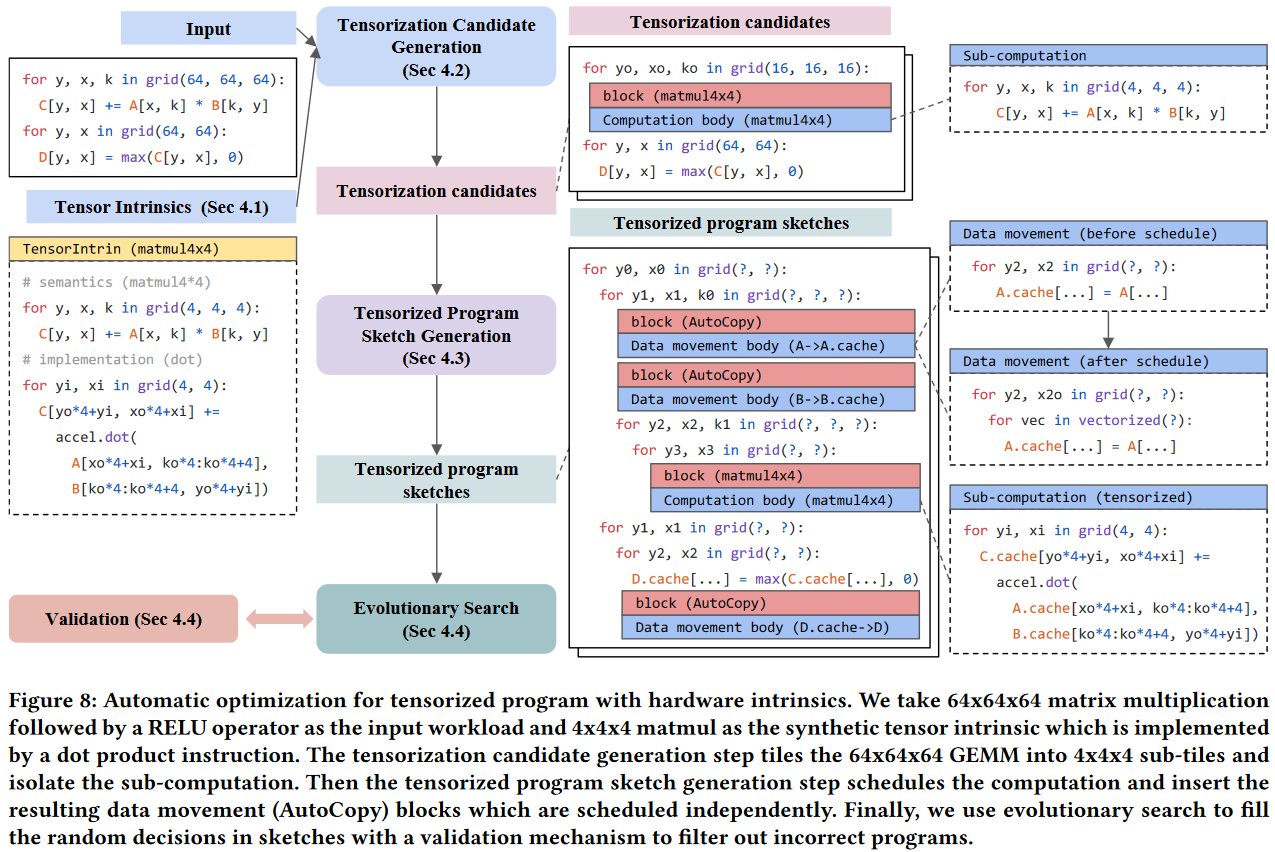引入AutoCopy块：将数据移动作为独立的优化目标、支持灵活的数据布局转换和缓存策略 端到端的优化流程：从高层程序到硬件指令的完整映射；自动处理计算和数据移动的优化

Tensorization Candidate Generation

ReIndex的目的是简化访问模式，通过引入中间缓冲区Ar和Br，将复杂的索引计算分解为两步

# 重组输入A的访问模式
Ar[n, h, w, rh, rw, rc] = A[n, h*2+rh, w*w+rw, rc]
# 重组卷积核B的访问
Br[c, rh, rw, rc] = B[c, rh, rw, rc]
# 最终计算
Cr[n, h, w, c] += Ar[n, h, w, rh, rw, rc] * Br[c, rh, rw, rc]

将卷积运算映射到矩阵乘法硬件指令

硬件指令的形式
C[x, y] += A[x, k] * B[k, y]
特征向量χ(v)表示一个迭代器v在不同缓冲区中的出现情况：对每个迭代器，生成一个二进制向量[是否在C中，是否在A中，是否在B中]；比如χ(n)=[1,1,0]表示n出现在C和A中，但不在B中
n, h, w: χ(n) = χ(h) = χ(w) = [1,1,0]
c:       χ(c) = [1,0,1]
rh, rw, rc: χ(rh) = χ(rw) = χ(rc) = [0, 1, 1]
与目标硬件指令对应
x: χ(x) = [1, 1, 0] # 对应n, h, w的模式
y: χ(y) = [1, 0, 1] # 对应c的模式
k: χ(k) = [0, 1, 1] # 对应rh,rw,rc的模式

根据上面的映射将n,h,w三个维度合并成一个维度、rh,rw,rc三个维度合并成一个维度，然后重写成如下操作

Ct[fuse(n,h,w), c] += At[fuse(n,h,w), fuse(rh,rw,rc)] * Bt[fuse(rh,rw,rc), c]

Tensorized Program Sketch Generation

Computation Schedule & Data Movement 传统优化中，计算和数据移动的时间差距较小，使用张量运算原语后，差距显著增大；如果不专门优化数据移动，很容易出现计算单元空闲等待数据的情况

# 原始代码
for i in range(64):
    for j in range(64):
        C[i, j] = A[i, j] + B[i, j]

# 计算调度优化
for i_outer in range(0, 64, 16):
    for j_outer in range(0, 64, 16):
        for i_inner in range(16):
            for j_inner in range(16):
                i = i_outer + i_inner
                j = j_outer + j_inner
                C[i, j] = A[i, j] + B[i, j]

# 数据移动优化
for i_outer in range(0, 64, 16):
    for j_outer in range(0, 64, 16):
        # 数据移动：加载到共享内存
        A_shared = load_to_shared_memory(A[i_outer:i_outer+16, j_outer:j_outer+16])
        B_shared = load_to_shared_memory(B[i_outer:i_outer+16, j_outer:j_outer+16])

        # 计算使用共享内存中的数据
        for i_inner in range(16):
            for j_inner in range(16):
                i = i_outer + i_inner
                j = j_outer + j_inner
                C[i, j] = A_shared[i_inner, j_inner] + B_shared[i_innner, j_inner]

Evaluation

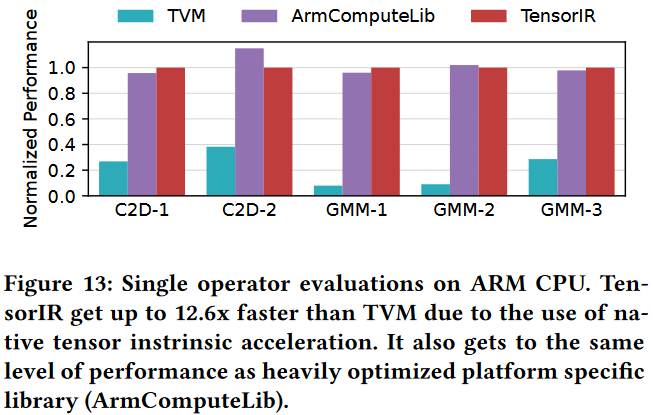
Single Operator Evaluation

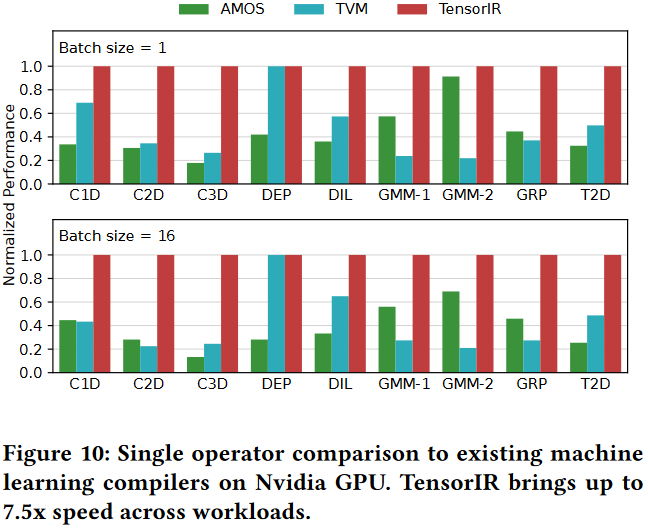
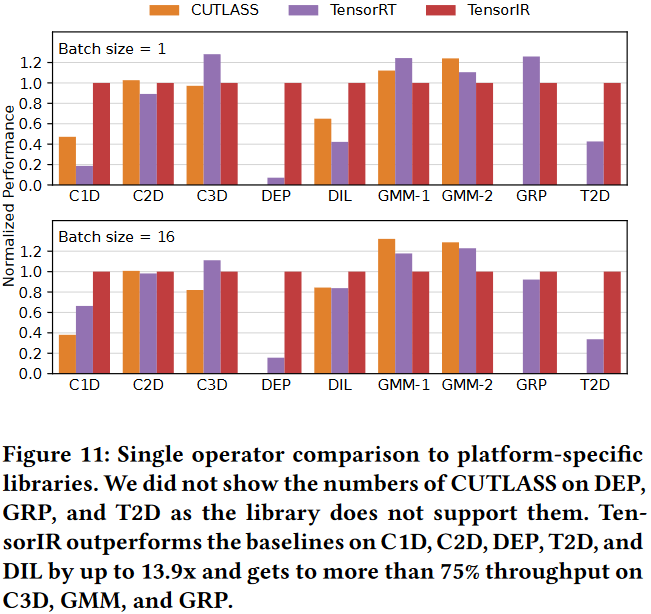
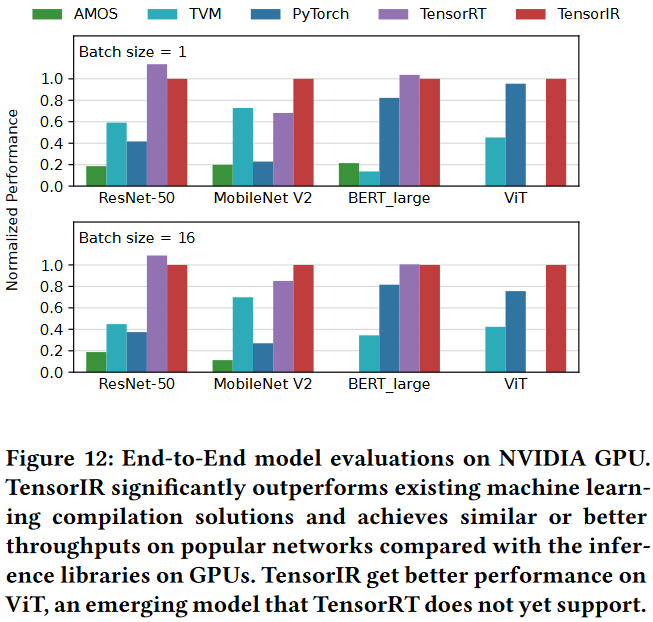
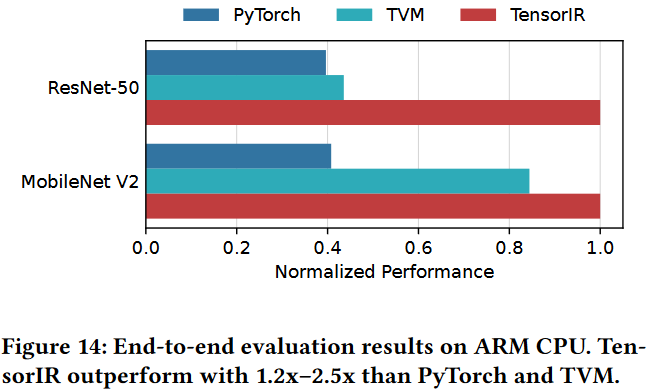
End-to-End Model Evaluation

ARM CPU Evaluation

Thinking

(1) 自动调度器的限制 (2) tensorization候选生成的局限 (3) 数据移动优化

Reference

TensorIR: An Abstraction for Automatic Tensorized Program Optimization

CATALOG
    FEATURED TAGS
    Tensor Compiler Compiler Optimization Code Generation Heterogeneous Systems Operator Fusion Deep Neural Network Recursive Tensor Execution Deep Learning Compiler Classical Machine Learning Compiler Optimizations Bayesian Optimization Autotuning Spatial Accelerators Tensor Computations Code Reproduction Neural Processing Units Polyhedral Model Auto-tuning Machine Learning Compiler Neural Network Program Transformations Tensor Programs Deep learning Tensor Program Optimizer Search Algorithm Compiler Infrastructure Scalalbe and Modular Compiler Systems Tensor Computation GPU Task Scheduling GPU Streams Tensor Expression Language Automated Program optimization Framework AI compiler memory hierarchy data locality tiling fusion polyhedral model scheduling domain-specific architectures memory intensive TVM Sparse Tensor Algebra Sparse Iteration Spaces Optimizing Transformations Tensor Operations Machine Learning Model Scoring AI Compiler Memory-Intensive Computation Fusion Neural Networks Dataflow Domain specific Language Programmable Domain-specific Acclerators Mapping Space Search Gradient-based Search Deep Learning Systems Systems for Machine Learning Programming Models Compilation Design Space Exploration Tile Size Optimization Performance Modeling High-Performance Tensor Program Tensor Language Model Tensor Expression GPU Loop Transformations Vectorization and Parallelization Hierarchical Classifier TVM API Optimizing Compilers Halide Pytorch Optimizing Tensor Programs Gradient Descent debug Automatic Tensor Program Tuning Operators Fusion Tensor Program Cost Model Weekly Schedule Spatio-temporal Schedule tensor compilers auto-tuning tensor program optimization compute schedules Tensor Compilers Data Processing Pipeline Mobile Devices Layout Transformations Transformer Design space exploration GPU kernel optimization Compilers Group Tuning Technique Tensor Processing Unit Hardware-software Codeisgn Data Analysis Adaptive Systems Program Auto-tuning python api Code Optimization Distributed Systems High Performance Computing code generation compiler optimization tensor computation Instructions Integration Code rewriting Tensor Computing DSL CodeReproduction Deep Learning Compiler Loop Program Analysis Nested Data Parallelism Compute-Intensive Automatic Exploration Loop Fusion Data Movement C++ Machine Learning System Decision Forest Optimizfing Compiler Decision Tree Ensemble Decision Tree Inference Parallelization Optimizing Compiler decision trees random forest machine learning parallel processing multithreading Tree Structure Performance Model Code generation Compiler optimization Tensor computation accelerator neural networks optimizing compilers autotuning performance models deep neural networks compilers auto-scheduling tensor programs Tile size optimization Performance modeling Program Functionalization affine transformations loop optimization Performance Optimization Subgraph Similarity deep learning compiler Intra- and Inter-Operator Parallelisms ILP tile-size operator fusion cost model graph partition zero-shot tuning tensor program kernel orchestration machine learning compiler Loop tiling Locality Polyhedral compilation Optimizing Transformation Sparse Tensors Asymptotic Analysis Automatic Scheduling Optimization Operation Fusion data reuse deep reuse Tensorize docker graph substitution compiler Just-in-time compiler graph Tensor program construction tensor compilation graph traversal Markov analysis Deep Learning Compilation Tensor Program Auto-Tuning Decision Tree Search-based code generation Domain specific lanuages Parallel architectures Dynamic neural network mobile device spatial accelerate software mapping reinforcement learning Computation Graph Graph Scheduling and Transformation Graph-level Optimization Operator-level Optimization Partitioning Algorithms IR Design Parallel programming languages Software performance Digitial signal processing Retargetable compilers Equational logic and rewriting Tensor-level Memory Management Code Generation and Optimizations Scheduling Sparse Tensor Auto-Scheduling Tensor Coarse-Grained Reconfigurable Architecture Graph Neural Network Reinforcement Learning Auto-Tuning Domain-Specific Accelerator Deep learning compiler Long context Memory optimization code analysis