EINNET OSDI 2023

Current solution

consider transfromations representable by a fixed set of predefined tensor operators
POR transformations:深度学习框架中已经内置的标准操作，如卷积、矩阵乘法、加法、激活函数—用积木搭建
General tensor algebra transformations:把操作拆解到更基础的数学表达式层面，可以生成全新的操作符—把积木拆开重新设计，创造处新的积木形状

The author’s proposal

exploer general tensor algebra transformations whose nodes are general tensor operators
面临的挑战：
(1) automatically discovering transformation opportunities between general expressions
(2) converting expressions back to kernels that be executed on DNN accelerators-expression instantiation
(3) quickly finding optimizing transformations in the search space of general tensor algebra transformations

Overview and Motivating Example

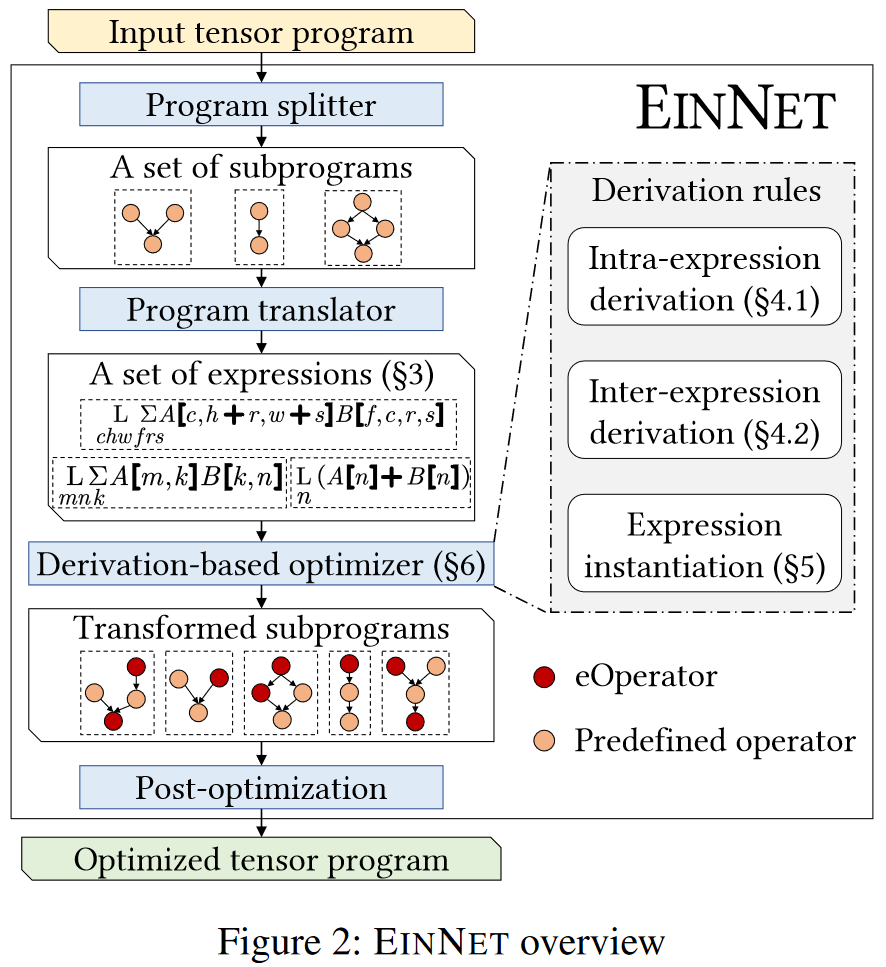
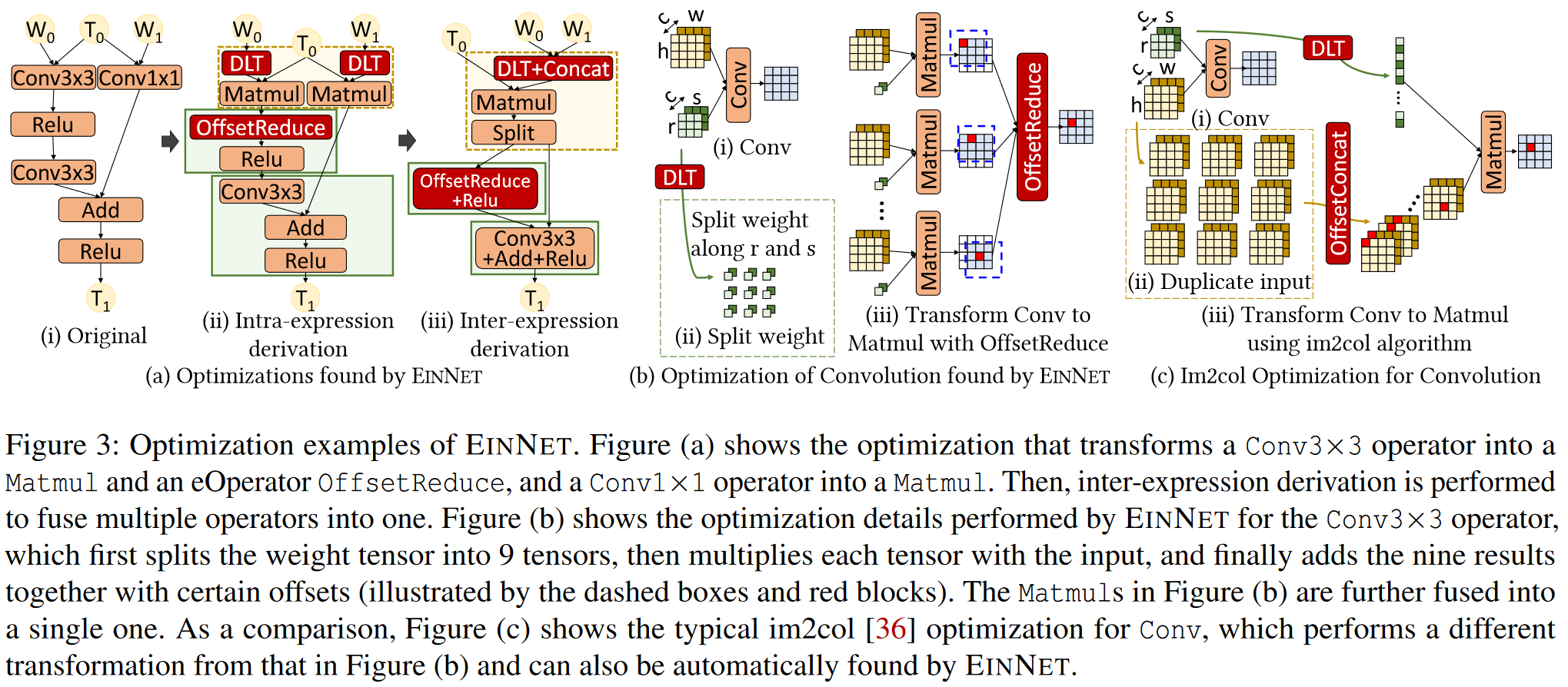
Derivation Rules

Intra-Expression Derivation

Summation splitting: 矩阵相乘AxBxC

A: [m x k]
B: [k x n]
C: [n x p]
未拆分
for i in range(m):
    for j in range(p):
        result[i, j] = 0
        for k in range(K):
            for n in range(N):
                result[i, j] += A[i, k] * B[k, n] * C[n, j]
拆分后
temp = np.zeros((m, n))
for i in range(m):
    for n in range(n):
        for k in range(k):
            temp[i, n] += A[i, k] * B[k, n]
result = np.zeros((m, p))
for i in range(m):
    for j in range(p):
        for n in range(n):
            result[i, j] += temp[i, n] * C[n, j]

Variable substitution

# 输入：input[H, W, C]
# 卷积核：kernel[3, 3, C, F]
# 输出: output[H, W, F]

原始表达式
for h in range(H):
    for w in range(W):
        for f in range(F):
            for r in range(3):
                for s in range(3):
                    for c in range(C):
                        output[h, w, f] += input[h+r, w+s, c] * kernel[r, s, c, f]
替换后的表达式
for f in range(F):
    # 遍历卷积核位置
    for r in range(3):
        for s range(3):
            for t1 in range(r, H+r):
                for t2 in range(s, W+s):
                    for c in range(C):
                        h = t1 - r
                        w = t2 - s
                        output[h, w, f] += input[t1, t2, c] * kernel[r, s, c, f]

Traversal merging 将矩阵A的每行先乘以一个系数v，然后与矩阵B相乘

未合并的表达式
for i in range(M):
    for j in range(N):
        temp = 0
        for k in range(K):
            scaled_a = {
                for _ in range(1):
                    scaled_a = A[i, k] * v[i]
            }

            temp += scaled_a * B[k, j]
        result[i, j] = temp
合并的表达式
for i in range(M):
    for j in range(N):
        temp = 0
        for k in range(K):
            temp += (A[i, k] * v[i]) * B[k, j]
        result[i, j] = temp

Expression Instantiation

将一个表达式匹配到已有的操作符，直接使用优化好的库比自己生成新代码更高效

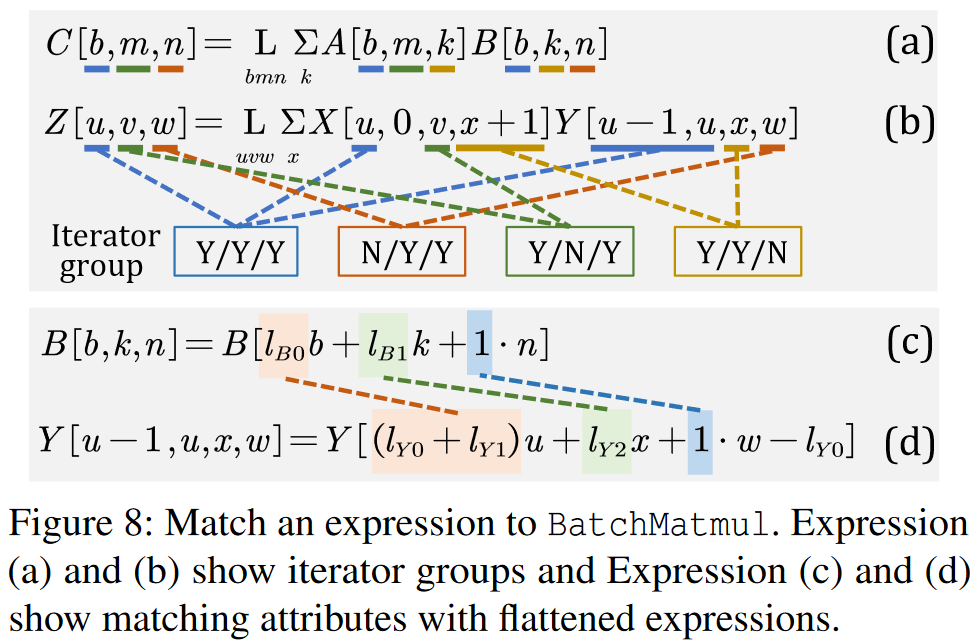
Operator Matching

match tensors
match iterators
match operator attributes

eOperator Generation

处理无法匹配到预定义操作符的表达式，利用off-the-shelf kernel generation framework(eg. TVM)

Program Optimizer

基于距离的搜索算法

Explorative derivation
Converging derivation (快速向目标操作符收敛) Expression distance: 使用迭代器映射表匹配两个表达式中的迭代器、统计不匹配的迭代器总数作为距离

Evaluation

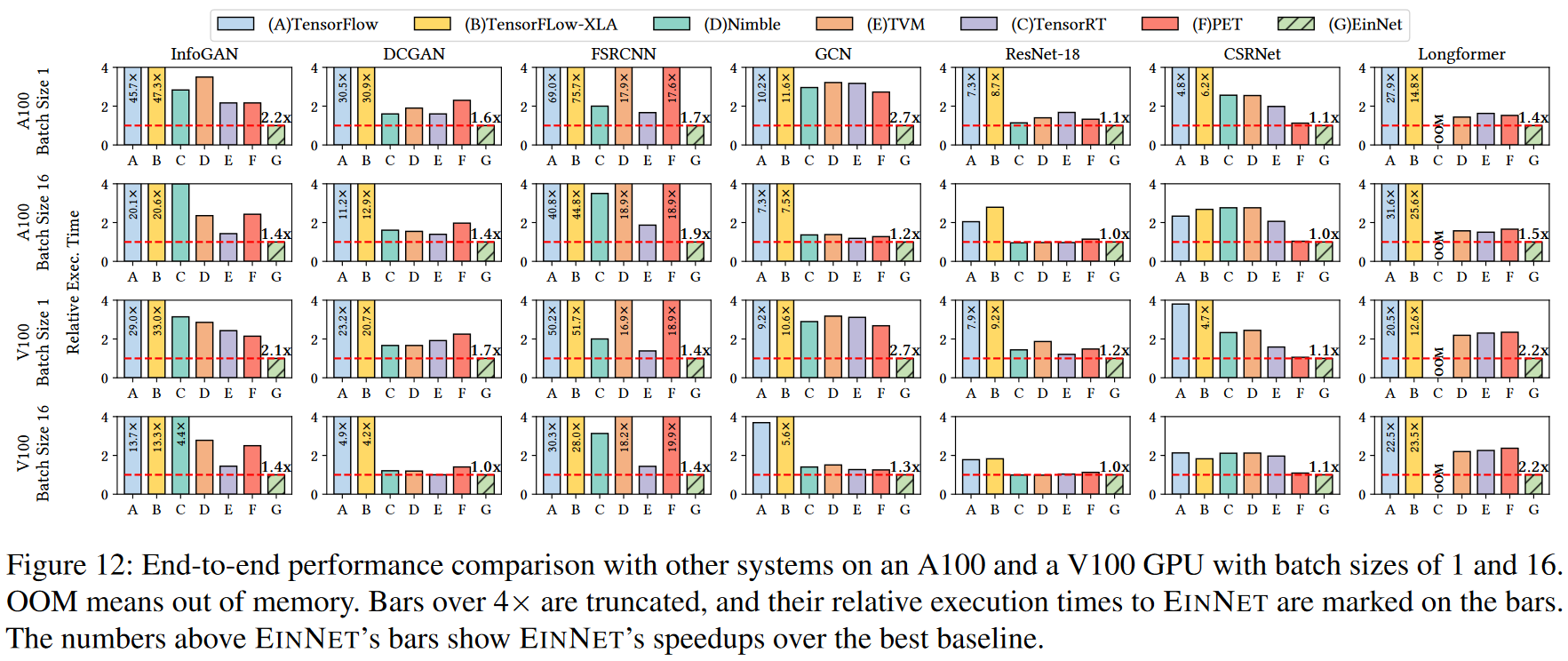
Thinking

(1) 只支持静态图，不支持动态图

静态图
# 批处理大小固定为32，输入维度固定为224*224
model = Model()
input = torch.randn(32, 3, 224, 224) #形状在编译时就确定
output = model(input)
动态图
# 批处理大小不固定，可能根据实际数据变化
model = Model()
batch_size = get_dynamic_batch_size()
input = torch.randn(batch_size, 3, 224, 224)
output = model(input)

(2) 本文主要关注计算优化，没有考虑内存带宽和缓存效应
(3) 相似的输入是否能得到相似的优化结果？
(4) 生成eOperator性能可能不如手工优化的版本(TVM)~~话说TVM生成效果不就是要比手工的好，但是在本文观点里面不一定比手工好~~

	PET	EINNET
核心思想	基于部分等价转换(partial equivalence)	基于张量代数表达式的推导
优化空间	预定义算子空间内	可推导出新算子
转换方式	图级别的模式匹配和替换	数学表达式推导生成
验证机制	需额外的修正机制	数学推导规则保证
性能提升来源	来自已知优化模式的应用	全新的优化机会

Reference

EINNET: Optimizing Tensor Programs with Derivation-Based Transformations

FEATURED TAGS

Tensor Compiler Compiler Optimization Code Generation Heterogeneous Systems Operator Fusion Deep Neural Network Recursive Tensor Execution Deep Learning Compiler Classical Machine Learning Compiler Optimizations Bayesian Optimization Autotuning Spatial Accelerators Tensor Computations Code Reproduction Neural Processing Units Polyhedral Model Auto-tuning Machine Learning Compiler Neural Network Program Transformations Tensor Programs Deep learning Tensor Program Optimizer Search Algorithm Compiler Infrastructure Scalalbe and Modular Compiler Systems Tensor Computation GPU Task Scheduling GPU Streams Tensor Expression Language Automated Program optimization Framework AI compiler memory hierarchy data locality tiling fusion polyhedral model scheduling domain-specific architectures memory intensive TVM Sparse Tensor Algebra Sparse Iteration Spaces Optimizing Transformations Tensor Operations Machine Learning Model Scoring AI Compiler Memory-Intensive Computation Fusion Neural Networks Dataflow Domain specific Language Programmable Domain-specific Acclerators Mapping Space Search Gradient-based Search Deep Learning Systems Systems for Machine Learning Programming Models Compilation Design Space Exploration Tile Size Optimization Performance Modeling High-Performance Tensor Program Tensor Language Model Tensor Expression GPU Loop Transformations Vectorization and Parallelization Hierarchical Classifier TVM API Optimizing Compilers Halide Pytorch Optimizing Tensor Programs Gradient Descent debug Automatic Tensor Program Tuning Operators Fusion Tensor Program Cost Model Weekly Schedule Spatio-temporal Schedule tensor compilers auto-tuning tensor program optimization compute schedules Tensor Compilers Data Processing Pipeline Mobile Devices Layout Transformations Transformer Design space exploration GPU kernel optimization Compilers Group Tuning Technique Tensor Processing Unit Hardware-software Codeisgn Data Analysis Adaptive Systems Program Auto-tuning python api Code Optimization Distributed Systems High Performance Computing code generation compiler optimization tensor computation Instructions Integration Code rewriting Tensor Computing DSL CodeReproduction Deep Learning Compiler Loop Program Analysis Nested Data Parallelism Compute-Intensive Automatic Exploration Loop Fusion Data Movement C++ Machine Learning System Decision Forest Optimizfing Compiler Decision Tree Ensemble Decision Tree Inference Parallelization Optimizing Compiler decision trees random forest machine learning parallel processing multithreading Tree Structure Performance Model Code generation Compiler optimization Tensor computation accelerator neural networks optimizing compilers autotuning performance models deep neural networks compilers auto-scheduling tensor programs Tile size optimization Performance modeling Program Functionalization affine transformations loop optimization Performance Optimization Subgraph Similarity deep learning compiler Intra- and Inter-Operator Parallelisms ILP tile-size operator fusion cost model graph partition zero-shot tuning tensor program kernel orchestration machine learning compiler Loop tiling Locality Polyhedral compilation Optimizing Transformation Sparse Tensors Asymptotic Analysis Automatic Scheduling Optimization Operation Fusion data reuse deep reuse Tensorize docker graph substitution compiler Just-in-time compiler graph Tensor program construction tensor compilation graph traversal Markov analysis Deep Learning Compilation Tensor Program Auto-Tuning Decision Tree Search-based code generation Domain specific lanuages Parallel architectures Dynamic neural network mobile device spatial accelerate software mapping reinforcement learning Computation Graph Graph Scheduling and Transformation Graph-level Optimization Operator-level Optimization Partitioning Algorithms IR Design Parallel programming languages Software performance Digitial signal processing Retargetable compilers Equational logic and rewriting Tensor-level Memory Management Code Generation and Optimizations Scheduling Sparse Tensor Auto-Scheduling Tensor Coarse-Grained Reconfigurable Architecture Graph Neural Network Reinforcement Learning Auto-Tuning Domain-Specific Accelerator Deep learning compiler Long context Memory optimization code analysis

EINNET Optimizing Tensor Programs with Derivation-Based Transformations