要解决的问题
在不同的硬件平台上,设计高性能tensor program对于不同算法十分困难,由于目前有限的搜索空间和低效的搜索策略
已有的解决方案
- predefined manually-written templates (TVM、FlexTensor)
- aggressive pruning by evaluating incomplete programs (Halide auto-scheduler)
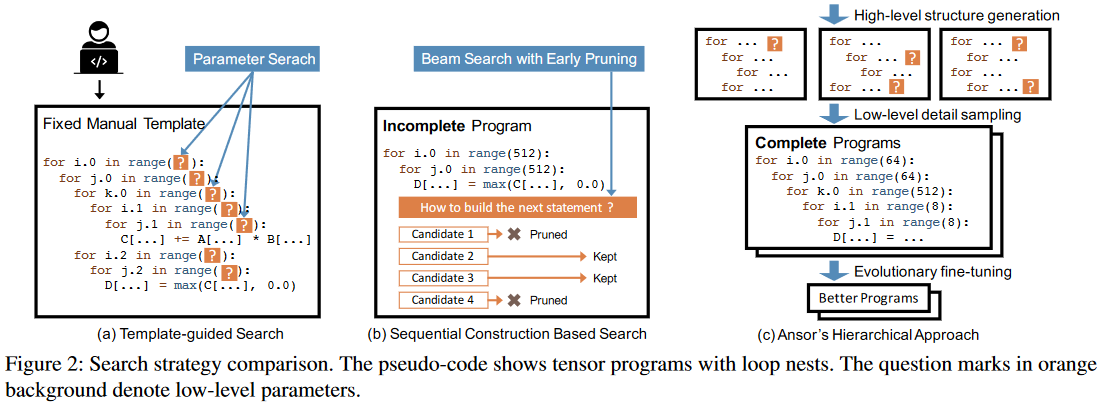
存在的问题:
1. TVM FlexTensor
需要大量人工编写模板、搜索空间受限于手写模板、难以支持新算子和硬件
2. Halide
评估困难、决策顺序固定、错误传播
新的解决方案
面临的挑战:
(1) constructing a large search space for a given computation definition-a hierarchical representation
(2) search efficiently-evolutionary search and a learned cost model
(3) recognize and prioritize the subgraphs that are critical to the end-to-end performance (对每个子图进行优化组合会导致次优性能?)(有些子图的优化对于性能提升无太大作用)-a task scheduler
Design
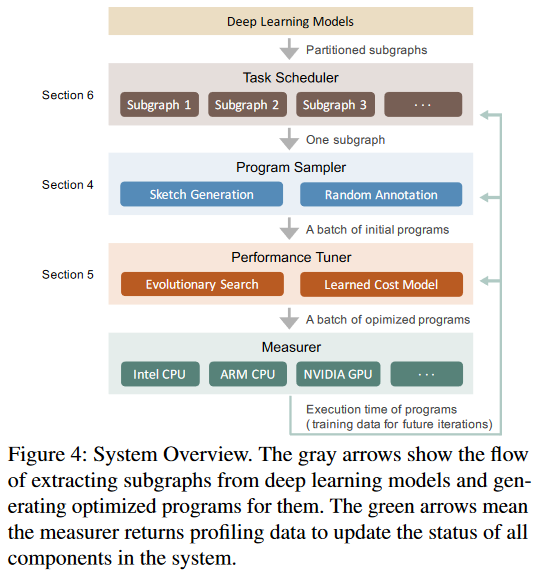
Program Sampling
(1) Sketch Generation
# 步骤1: 按拓扑序访问DAG中的节点
for node in topological_order(DAG):
# 步骤2:根据节点类型选择处理方式
if is_compute_intensive(node): # 计算密集型节点(如conv2d,matmul)
build_tile_and_fusion_structure(node)
elif is_element_wise(node): # 简单的逐元素操作(如ReLU,add)
inline_node(node)
处理规则
rule-1 skip 直接跳到下一个节点
# 例如处理一个复杂的卷积节点,由于卷积操作复杂,不能内联,所以直接跳过
for i, j in range(H, W):
conv2d[i,j] = complex_computation()
# 跳过后保持原样,继续处理下一个节点
rule-2 always inline
# 原始代码
t1 = relu(x)
t2 = t1 + y
#内联后
t2 = relu(x) + y
rule-3 multi-level tiling 多级分块规则
# 原始矩阵乘法
for i, j, k in range(N, M, K):
C[i, j] += A[i, k] * B[k, j]
# 应用多级分块后
for i0 in range(N//64): # 空间循环S
for j0 in range(M//64): # 空间循环S
for k0 in range(k//32): # 归约循环R
for i1 in range(64): # 空间循环S
for k1 in range(32): # 归约循环R
for j1 in range(64):# 空间循环S
C[i0*64+i1, j0*64+j1] += A[i0*64+i1, k0*32+k1] * B[k0*32+k1, j0*64+j1]
rule-4 multi-level tiling with fusion
# 原始代码
# 1. 矩阵乘法
for i, j, k:
C[i, j] += A[i, k] * B[k, j]
# 2. ReLU操作
for i, j:
D[i, j] = relu(C[i, j])
#融合后的代码
for i0, j0:
for i1, j1:
for k:
# 矩阵乘法和ReLU在同一个循环内完成
C[i0*64+i1, j0*64+j1] += A[i0*64+i1, k] * B[k, j0*64+j1]
D[i0*64+i1, j0*64+j1] = relu(C[i0*64+i1, j0*64+j1])
rule-5 add cache stage
# 原始代码
for i, j, k:
C[i, j] += A[i, k] * B[k, j]
# 添加缓存后
# 1. 计算并写入缓存
for i0, j0:
cache[i0, j0] = compute_block(A, B, i0, j0)
# 2. 从缓存写回内存
for i0, j0:
C[i0:i0+block, j0:j0+block] = cache[i0, j0]
rule-6 reduction factorization
# 原始代码 - 计算矩阵每列的和
for j in range(N):
for i in range(M):
sum[j] += matrix[i, j]
# 分解后 - 引入中间结果实现并行
# 1. 并行计算部分和
parallel for b in range(B):
for j in range(N):
for i in range(b*M//B, (b+1)*M//B):
partial_sum[b, j] += matrix[i, j]
# 2. 归约部分和得到最终结果
for j in range(N):
for b in range(B):
sum[j] += partial_sum[b, j]
Example

Evaulation
Single operator 👉 Subgraph 👉 End-to-end network
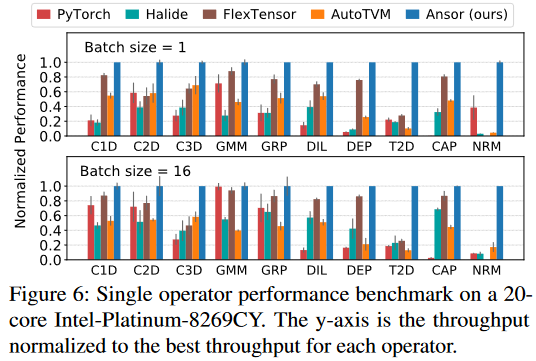
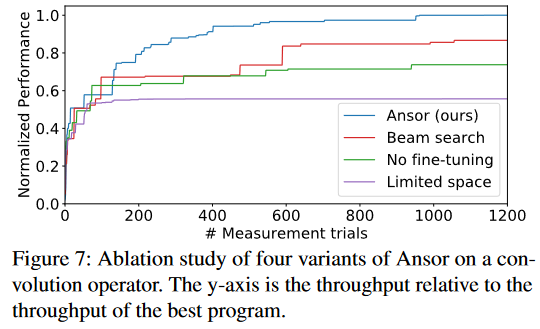
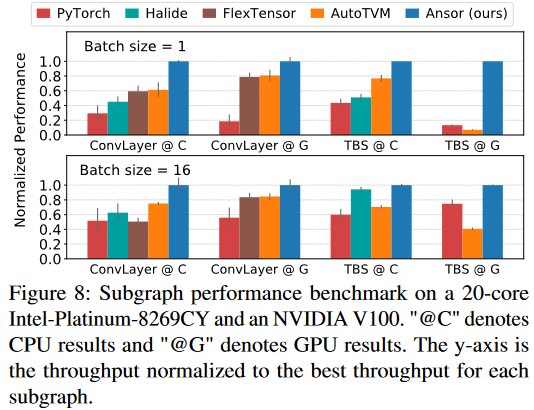


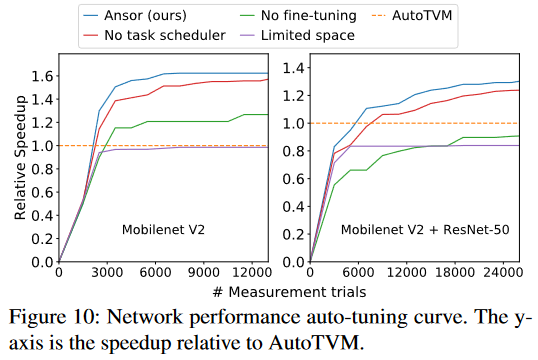
search time

思考
参考文献
Ansor: Generating High-Performance Tensor Programs for Deep Learning
FEATURED TAGS
Genetic Algorithm
Multi-objective Optimization
Instruction-Level Parallelism(ILP)
Compiler
Deep Learning Accelerators
Tensor Compiler
Compiler Optimization
Code Generation
Heterogeneous Systems
Operator Fusion
Deep Neural Network
Recursive Tensor Execution
Deep Learning
Classical Machine Learning
Compiler Optimizations
Bayesian Optimization
Autotuning
Spatial Accelerators
Tensor Computations
Code Reproduction
Neural Processing Units
Polyhedral Model
Auto-tuning
Machine Learning Compiler
Neural Network
Program Transformations
Tensor Programs
Deep learning
Tensor Program Optimizer
Search Algorithm
Compiler Infrastructure
Scalalbe and Modular Compiler Systems
Tensor Computation
GPU Task Scheduling
GPU Streams
Tensor Expression Language
Automated Program optimization Framework
AI compiler
memory hierarchy
data locality
tiling fusion
polyhedral model
scheduling
domain-specific architectures
memory intensive
TVM
Sparse Tensor Algebra
Sparse Iteration Spaces
Optimizing Transformations
Tensor Operations
Machine Learning
Model Scoring
AI Compiler
Memory-Intensive Computation
Fusion
Neural Networks
Dataflow
Domain specific Language
Programmable Domain-specific Acclerators
Mapping Space Search
Gradient-based Search
Deep Learning Systems
Systems for Machine Learning
Programming Models
Compilation
Design Space Exploration
Tile Size Optimization
Performance Modeling
High-Performance Tensor Program
Tensor Language Model
Tensor Expression
GPU
Loop Transformations
Vectorization and Parallelization
Hierarchical Classifier
TVM API
Optimizing Compilers
Halide
Pytorch
Optimizing Tensor Programs
Gradient Descent
debug
Automatic Tensor Program Tuning
Operators Fusion
Tensor Program
Cost Model
Weekly Schedule
Spatio-temporal Schedule
tensor compilers
auto-tuning
tensor program optimization
compute schedules
Tensor Compilers
Data Processing Pipeline
Mobile Devices
Layout Transformations
Transformer
Design space exploration
GPU kernel optimization
Compilers
Group Tuning Technique
Tensor Processing Unit
Hardware-software Codeisgn
Data Analysis
Adaptive Systems
Program Auto-tuning
python api
Code Optimization
Distributed Systems
High Performance Computing
code generation
compiler optimization
tensor computation
Instructions Integration
Code rewriting
Tensor Computing
DSL
CodeReproduction
Deep Learning Compiler
Loop Program Analysis
Nested Data Parallelism
Loop Fusion
C++
Machine Learning System
Decision Forest
Optimizfing Compiler
Decision Tree Ensemble
Decision Tree Inference
Parallelization
Optimizing Compiler
decision trees
random forest
machine learning
parallel processing
multithreading
Tree Structure
Performance Model
Code generation
Compiler optimization
Tensor computation
accelerator
neural networks
optimizing compilers
autotuning
performance models
deep neural networks
compilers
auto-scheduling
tensor programs
Tile size optimization
Performance modeling
Program Functionalization
affine transformations
loop optimization
Performance Optimization
Subgraph Similarity
deep learning compiler
Intra- and Inter-Operator Parallelisms
ILP
tile-size
operator fusion
cost model
graph partition
zero-shot tuning
tensor program
kernel orchestration
machine learning compiler
Loop tiling
Locality
Polyhedral compilation
Optimizing Transformation
Sparse Tensors
Asymptotic Analysis
Automatic Scheduling
Data Movement
Optimization
Operation Fusion
Compute-Intensive
Automatic Exploration
data reuse
deep reuse
Tensorize
docker
graph substitution
compiler
Just-in-time compiler
graph
Tensor program
construction tensor compilation
graph traversal
Markov analysis
Deep Learning Compilation
Tensor Program Auto-Tuning
Decision Tree
Search-based code generation
Domain specific lanuages
Parallel architectures
Dynamic neural network
mobile device
spatial accelerate
software mapping
reinforcement learning
Computation Graph
Graph Scheduling and Transformation
Graph-level Optimization
Operator-level Optimization
Partitioning Algorithms
IR Design
Parallel programming languages
Software performance
Digitial signal processing
Retargetable compilers
Equational logic and rewriting
Tensor-level Memory Management
Code Generation and Optimizations
Scheduling
Sparse Tensor
Auto-Scheduling
Tensor
Coarse-Grained Reconfigurable Architecture
Graph Neural Network
Reinforcement Learning
Auto-Tuning
Domain-Specific Accelerator
Deep learning compiler
Long context
Memory optimization
code analysis
transformer
architecture-mapping
DRAM-PIM
LLM